A detailed explanation of the red black tree

First, the introduction of red black trees

Red-black tree is a self-balancing binary search tree, which is an efficient search tree. It was invented by Rudolf Bayer in 1972 and was called symmetric binary B-trees at the time. Later, in 1978, it was modified by Leo J. Guibas and Robert Sedgewick into today's red-black trees. The red-black tree has good efficiency, and it can find, add, delete, etc. in O(logN) time. Therefore, the red-black tree is widely used in the industry. For example, TreeMap in Java, HashMap in JDK 1.8, and map in C++ STL are all based on the red-black tree structure. Considering that red-black trees are a widely used data structure, it is necessary to understand it.

"

Second, the nature of red and black trees

Students who have studied the binary search tree know that the ordinary binary search tree can be degraded into a linked list in extreme cases, and the efficiency of addition and deletion will be relatively low at this time. In order to avoid this situation, there are some self-balancing search trees, such as AVL, red black trees and so on. These self-balancing search trees control the height difference between the left and right subtrees of any node by defining some properties to achieve equilibrium. Taking red-black trees as an example, red-black trees achieve self-balancing by defining the following properties:

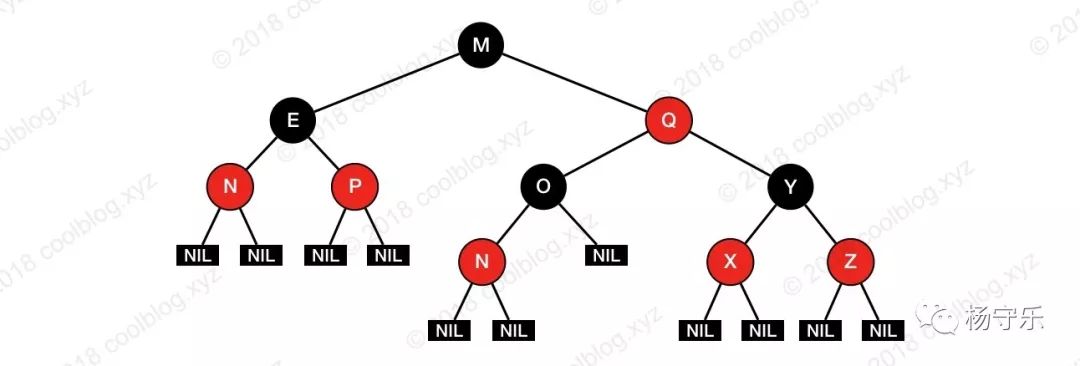
The node is red or black.

The root is black.

All leaves are black (leaves are NIL nodes).

Each red node must have two black children. (You cannot have two consecutive red nodes on all paths from each leaf to the root.)

All simple paths from any node to each of its leaves contain the same number of black nodes (black high).

With the above several properties as a limitation, it is possible to avoid the case where the binary search tree is degenerated into a single linked list. However, just avoiding this situation is not enough, here also consider the problem of the length of a node to the path length of each of its leaf nodes. If some paths are too long, the efficiency will be greatly reduced when adding and deleting operations on these paths. At this time, the use of nature 4 and nature 5 is highlighted. With these two properties as constraints, it is guaranteed that the path from any node to each of its leaf nodes will not exceed 2 times the shortest path. The reasons are as follows:

When a path is the shortest, this path must be composed of black nodes. When a path has the longest length, this path must be composed of red and black nodes (the nature 4 defines that two consecutive red nodes cannot appear). Property 5, in turn, defines that all paths from any node to each of its leaf nodes must contain the same number of black nodes. At this time, in the case where the path is the longest, the number of red nodes on the path = the number of black nodes. The path length is twice the number of black nodes, which is twice the length of the shortest path. For an example, please see the picture below:

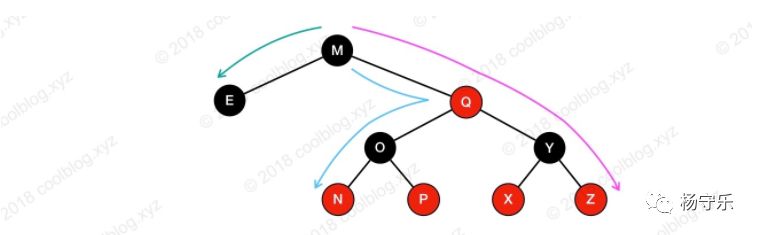
The picture shows the longest and shortest path from the root node M to its leaf nodes. The lazy here only draws the two longest paths. In fact, the longest path has four, which are:

M -> Q -> O -> N

M -> Q -> O -> p

M -> Q -> Y -> X

M -> Q -> Y -> Z

The length is 4, the shortest path is M -> E, and the length is 2. The length of the longest path is exactly twice the length of the shortest path.

I mentioned some about the nature of red and black trees. There are some other things that need to be added here. In the introduction to the red-black tree, it is said that the red-black tree was not called the red-black tree when it was invented, but it was called the symmetric binary B-tree. From the name, you can find the red-black tree and the B-tree (here refers to 2-3 trees) may have a certain connection, and this is also the case. If the nature of the red-black tree is slightly modified, the red-black tree and the B-tree can be formed in a one-to-one correspondence. The details about the relationship between the red-black tree and the B-tree are not explained here. Interested students can refer to the fourth edition of Algorithms, which is very thorough in the book.

"

Third, the red black tree operation

The basic operation of a red-black tree is the same as other tree structures, and generally includes operations such as finding, inserting, and deleting. As mentioned above, the red-black tree is a self-balancing binary search tree. Since it is a kind of binary search tree, the search process is the same as the binary search tree, which is relatively simple and will not be described here. The insertion and deletion of red-black trees is much more complicated than the lookup operation. Especially in the deletion operation, there are many situations to deal with, but if you calm down and look at it, you will find that it is not so difficult. Ok, let's talk about it in nonsense, then step into the topic.

3.1 Rotation operation

Before analyzing the insert and delete operations, you need to insert a team here, first explain the rotation operation, this operation will be used in subsequent operations. The rotation operation is divided into a left-handed and a right-handed rotation, the left-handed rotation is a left child of a right child, and the right-handed rotation is a right child of the left child. This sounds a bit winding, so please take a look at the picture below:

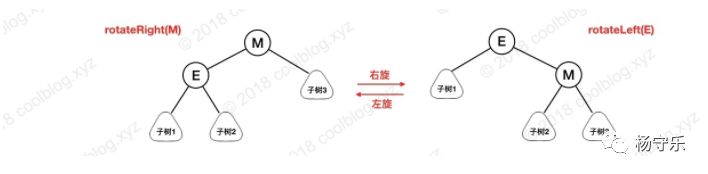
The figure above contains a schematic diagram of left-handed and right-handed. Here, the right-handed rotation is taken as an example. The steps of right-handed node M are as follows:

1. Point the left child of node M to the right child of node E.

2. Point the right child of node E to node M and complete the rotation.

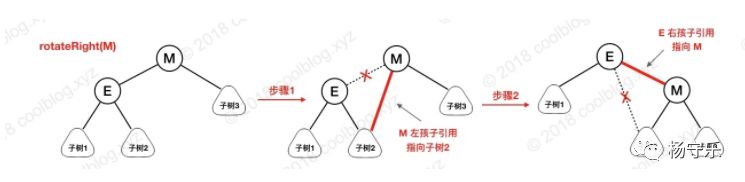
The above analysis of the right-handed operation, the left-handed operation is similar to this, everyone is interested in drawing their own pictures, so I won't go into details here. The rotation itself is not complicated, so let's analyze it first.

3.2 Insert

The insertion process of the red-black tree is basically similar to the binary search tree insertion process. The difference is that after the red-black tree is inserted into the new node, it needs to be adjusted to meet the nature of the red-black tree. Property 1 specifies that the color of the red-black tree node is either red or black, so when the new node is inserted, should the node be red or black? The answer is red, and the reason is not difficult to understand. If the inserted node is black, then the path of this node is one more black than the other paths. This adjustment will be more troublesome (refer to the deletion operation of the red-black tree, it is known that when one or more black nodes are used, the adjustment is made. It’s so troublesome.) If the inserted node is red, the number of black nodes on all paths is unchanged at this time, and only two consecutive red nodes may occur. In this case, adjustment can be made by discoloration and rotation, which is much simpler than before.

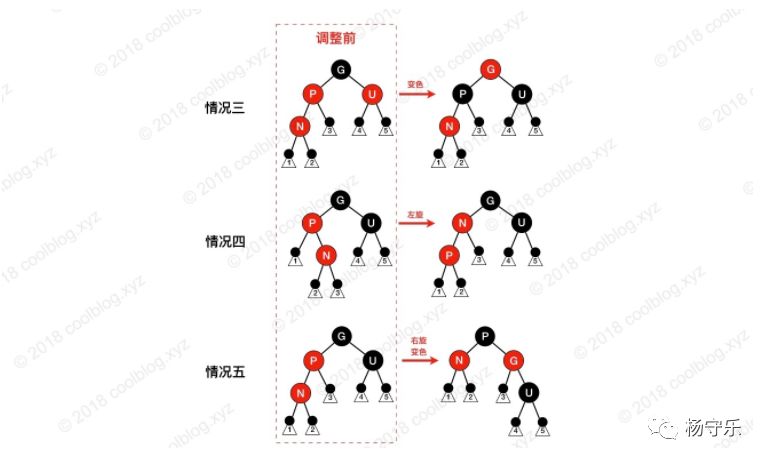
Next, the situation of the red-black tree after the red node is inserted will be analyzed. It is assumed here that the node to be inserted is N, the parent node of N is P, the grandparent node is G, and the uncle node is U. After inserting the red node, there will be 5 cases, as follows:

Case 1:

The inserted new node N is the root node of the red-black tree. In this case, we change the color of node N from red to black, and property 2 (root is black) is satisfied. At the same time N is dyed black, the number of black nodes on all paths of the red-black tree is increased by one, and the property 5 (all simple paths from any node to each of its leaves contain the same number of black nodes) is still satisfied.

Case 2:

The parent node of N is black, in this case, property 4 (each red node must have two black child nodes) and property 5 is unaffected and does not need to be adjusted.

Case 3: The parent node of N is red (node ​​P is red, its parent must be black), and the uncle node U is also red. Since both P and N are red, all properties 4 are broken and adjustments are needed. In this case, first dye the colors of P and U to black, and then dye the color of G to red. At this time, the number of black nodes on the path passing through G is unchanged, and the property 5 is still satisfied. However, it should be noted that after G is dyed red, it may form a continuous red node with its parent node, which requires recursive upward adjustment.

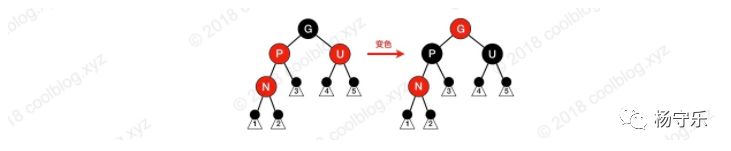
Situation 4:

The parent node of N is red, and the uncle node is black. Node N is the right child of P, and node P is the left child of G. At this point, first rotate the node P to adjust the position of N and P. Next, proceed according to Case 5 to restore the property 4.

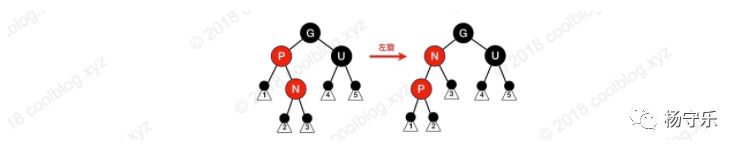
It is necessary to specify here that the node N in the above figure is not the newly inserted node. When P is red, P has two child nodes, and the child nodes are all black, so that the number of black nodes on the path from G to each leaf node can be consistent. Since P already has two children, N is not a newly inserted node. In the fourth case, a new node is inserted into the subtree with N as the root node. After adjustment, N is turned red, which leads to the occurrence of case four. Consider the following scenario (the PR node is the N node of the above figure):

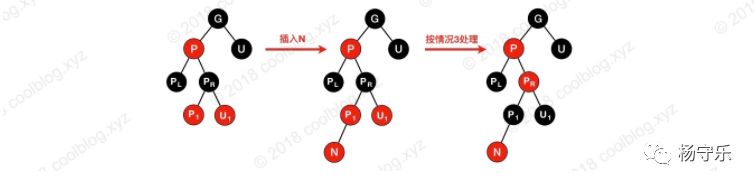
As shown above, insert node N and process it as per case three. At this point, the PR is dyed red, forming a continuous red node with the P node. At this time, it needs to be adjusted again according to the situation 4.

Case 5:

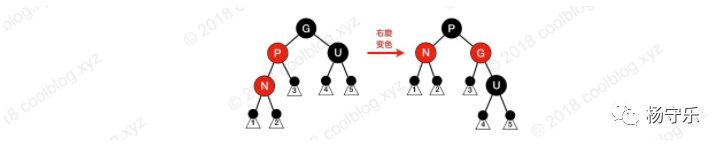
The parent node of N is red, and the uncle node is black. N is the left child of P, and node P is the left child of G. At this point, G is right-handed, the positions of P and G are adjusted, and the colors are interchanged. After such an adjustment, the property 4 is restored without destroying the property 5.

Insert summary

In the above five cases, Case 1 and Case 2 are relatively simple, and Cases 3, 4, and 5 are slightly more complicated. However, if you look carefully, you will find that the difference between the three conditions is the color of the uncle node. If the uncle node is red, you can change color directly. If the uncle node is black, you need to choose and exchange colors. When the pictures of these three situations are together, the difference is easier to observe, as shown below:

3.3 delete

The deletion of the red-black tree is more complicated than the insert operation. The deletion operation first determines that there are several children in the node to be deleted. If there are two children, the node cannot be deleted directly. Instead, first find the precursor of the node (the largest node in the left subtree of the node) or the successor (the smallest node in the right subtree of the node), and then copy the predecessor or subsequent values ​​to the node to be deleted, and finally Then remove the precursor or successor. Since the predecessor and the successor have at most one child node, we have turned the problem that the original node to be deleted has two children into a problem with only one child node, and the problem is simplified. We don't care if the node that was eventually deleted is the one we want to delete, as long as the values ​​in the node are finally deleted. It doesn't matter how the tree structure changes.

The complexity of the red-black tree deletion operation is to delete the color of the node. When the deleted node is red, the child node can be directly filled with the empty space. Because the red node is deleted, property 5 (all simple paths from either node to each of its leaves contain the same number of black nodes) can still be satisfied. When the deleted node is black, then the number of black nodes on all paths passing through the node is one less, destroying the property 5. If the child of the node is red, replace the deleted node with the child node directly, and dye the child node black, then the property 5 can be restored. But if the child node is black, it will be much more complicated to handle. There are 6 cases, which will be explained below.

Before we expand the instructions, let's make some assumptions for convenience. It is assumed here that the node that is finally deleted is X (at most there is only one child node), the child node is N, the sibling node of X is S, the left node of S is SL, and the right node is SR. The next discussion is based on the fact that node X is deleted and node N is replaced by X. Here, the reason for specifically deleting the deleted node X is to prevent everyone from thinking that the node N will be deleted, and then it will not be understood.

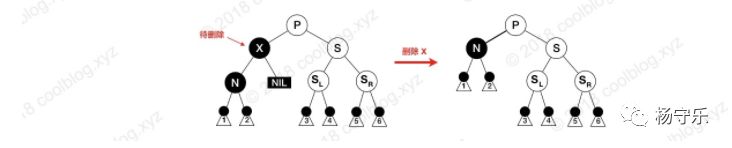
On the basis of the above, the discussion can be started next. There are 6 cases of red and black tree deletion, which are:

Case 1:

N is the new root. In this case, we are done. We removed a black node from all paths, and the new root is black, so the properties are maintained.

The above is a description of the situation of red black tree deletion in Wikipedia. Because there is no picture, it looks a little dizzy. After thinking, I think it might be the following situation:

The node X to be deleted is the root node, and the left and right child nodes are all empty nodes. At this time, the node X is replaced with an empty node to complete the deletion operation.

There may be other situations, if you know, please let me know.

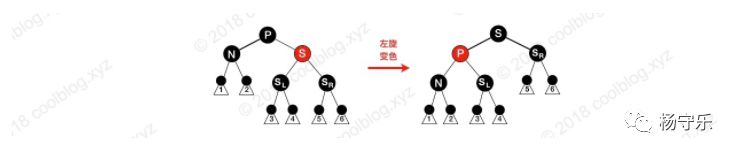
Case 2:

S is red and the other nodes are black. In this case, the parent node of N can be left-handed and then the P and S colors can be interchanged. But this is not the end. There are 3 black nodes (P -> X -> N) before the path of nodes P and N are deleted. Now there are only two left (P -> N). There is one black node less than the path without N, and the property 5 is still not satisfied, and it needs to be adjusted. However, at this time, adjustments can be made according to the situation four, five, and six.

Case 3:

The parent node of N, the child nodes of sibling nodes S and S are all black. In this case, S can be simply dyed red, and all paths passing through S are one black node less than before, so that the path through N is the same as the number of black nodes passing through S. However, the path through P is one less black than the path without P. In this case, P needs to be balanced from the beginning of the situation.

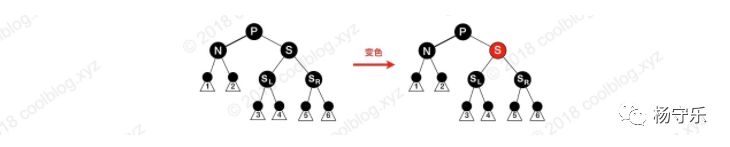
Situation 4:

The parent node of N is red, and the children of S and S are black. This situation is relatively simple, we only need to exchange P and S colors. Thus, all black nodes are added to the path through N, and all the paths through the nodes of S must also pass through the P node. Since P and S are only interchangeable colors, they do not affect these paths.

Case 5:

S is black, the left child of S is red, and the right child is black. The parent color of N can be red or black, and N is the child of P left. In this case, S is right-handed and the colors of S and SL are interchanged. At this point, the number of blacks on all paths is still equal, the S of the N siblings changes to SL, and the right child of SL turns red. Next we continue to analyze in case six.

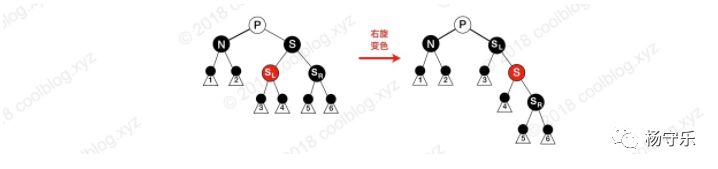
Situation 6:

S is black and the right child of S is red. The parent color of N can be red or black, and N is the parent of the parent node. In this case, we make a left-handed operation on P, swap the colors of P and S, and turn SR into black. Because P becomes black, there is one black node in the path through N, and the black node on the path through N is the same as the number before the deletion. For paths that do not pass N, there are two cases:

The path passes through the N new sibling node SL, which must pass S and P before. S and P are now just swapping colors, and they don't affect the path through SL.

The path passes through N's new uncle node S, which must pass P, S, and SR before, but now it only passes S and SR. After P is left-handed and replaced with S, the path through the SR is missing a black node and the property 5 is broken. In addition, since the color of S can be red or black, if S is red, it will form a continuous red node with SR, breaking the property 4 (each red node must have two black children). At this point, you only need to change the SR from red to black to restore both property 4 and property 5 (all simple paths from any node to each of its leaves contain the same number of black nodes.).

Delete summary

Red and black trees are deleted more often, and people may be more dizzy when they first start watching. There may be such a question, there will be such a deletion for the blushing black tree, and there will be another situation for å•¥, what are the connections and differences between them? Like everyone else, I was confused when I first started watching it. When I put together the graphics for all the situations, I saw the clouds and saw everything, and everything was clear. At this time, there were four words in the sky. It turned out to be the case. So please look at the picture:

"

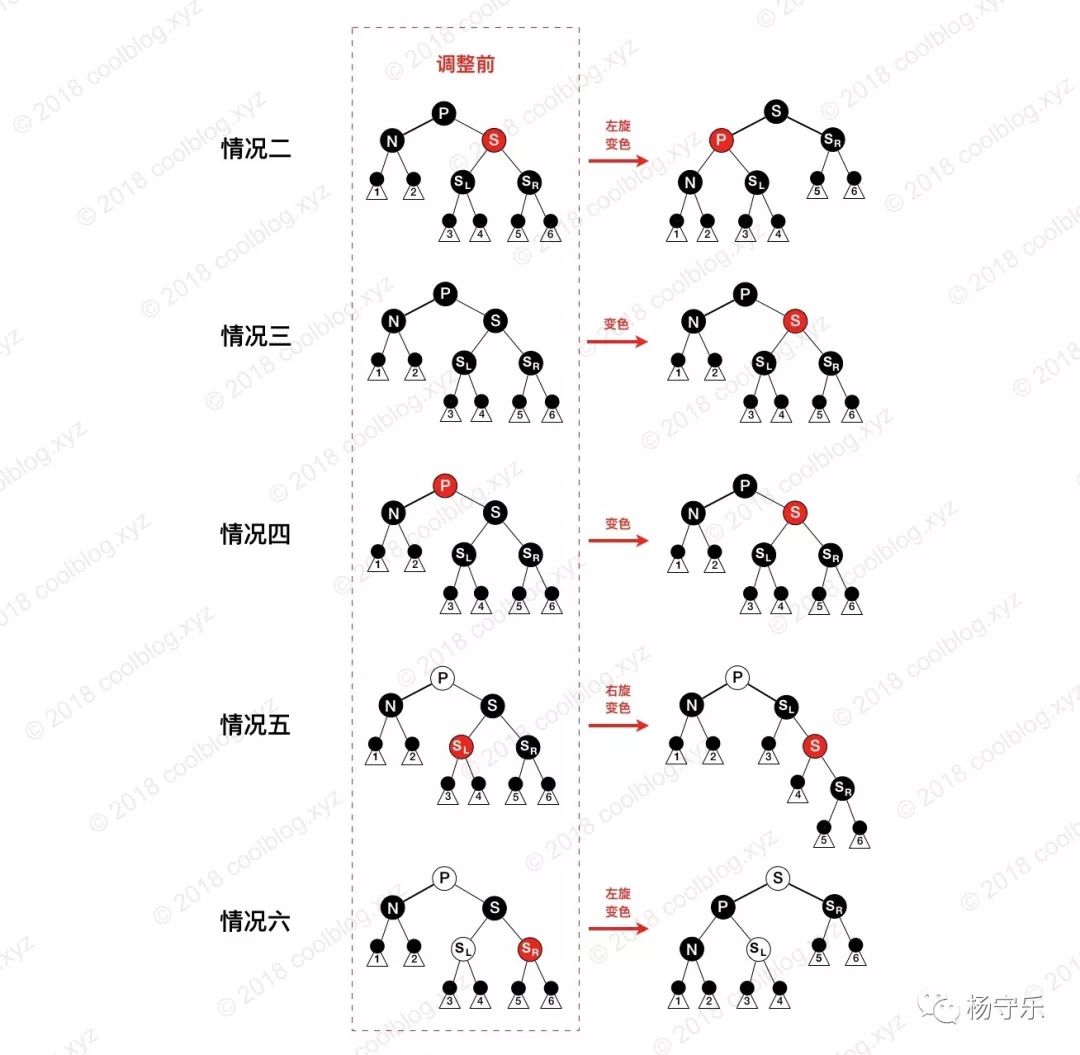
Fourth, summary

Red-black trees are an important binary tree that is widely used, but not many times in many data structure-related books. Many books either don't say it, or take it with you, and don't do detailed analysis. This may be because the red-black tree is more complicated. I also found a lot of information when I was studying red and black trees, but the overall feeling was not very good. Especially when I learn to delete the operation, a lot of information is invisible, and I am very painful to see. I was very happy until I saw the analysis of red and black trees on Wikipedia. The analysis of this article is very organized, concise, and much better than a lot of information. The analysis of red-black trees in this paper also mainly refers to the analysis of red-black trees in Wikipedia, and explains the problems that are easy to be questioned and misunderstood in Wikipedia. At the same time, the pictures in the black and white tree of the Wikipedia Chinese version are relatively vague, and I have redrawn it here. It should be noted that the Chinese version of Wikipedia cannot be opened. The links to Wikipedia in the article are all in English. In addition, we recommend a data structure visualization website, which contains the common data structure visualization process, the address is: https://~galles/visualization/Algorithms.html.

In addition, because the red-black tree itself is more complicated, the implementation is more complicated. Before writing this article, I tried to implement the addition and deletion of the red-black tree in the Java language. In the end, I only wrote the new node operation, and the deletion was not made. Moreover, the new logic written by myself is too cumbersome, the writing is not good-looking, and there is no face to show it. So finally copy and delete the relevant source code in TreeMap in Java, modify the source code according to your own needs, and barely calculate the red black tree. The following is the code RBTree.java.

Package search;import java.util.*;/** * Red Black Tree implementation, the core logic of the implementation is modified from the TreeMap source code * * @author code4wt * @date 2017-12-23 17:26:28 */public Class RBTree > { private final static boolean RED = true; private final static boolean BLACK = false; private TreeNode Root; public boolean contains(T value) { return Objects.nonNull(getNode(value)); } public void putAll(Collection Collection) { collection.forEach(this::put); } public void put(T value) { if (Objects.isNull(value)) { throw new NullPointerException(); } TreeNode t = root; if (Objects.isNull(t)) { root = new TreeNode<>(null, null, null, value); return; } int cmp; TreeNode Parent; do { parent = t; cmp = value.compareTo(t.value); if (cmp == 0) { return; } else if (cmp > 0) { t = t.right; } else { t = t .left; } } while (Objects.nonNull(t)); TreeNode e = new TreeNode<>(parent, null, null, value); if (cmp < 0) { parent.left = e; } else { parent.right = e; } fixAfterInsertion(e); } public void remove(T Value) { TreeNode p = getNode(value); if (Objects.nonNull(value)) { deleteNode(p); } } public void clear() { root = null; } private TreeNode getNode(T value) { if (Objects.isNull(value)) { throw new NullPointerException(); } TreeNode p = root; while (Objects.nonNull(p)) { int cmp = value.compareTo(p.value); if (cmp < 0) { p = p.left; } else if (cmp > 0) { p = P.right; } else { return p; } } return null; } private void deleteNode(TreeNode p) { // When node p has two child nodes, first find the successor node of the p node if (p.left != null && p.right != null) { TreeNode s = successor(p); p.value = s.value; p = s; } TreeNode Replacement = (p.left != null ? p.left : p.right); if (replacement != null) { replacement.parent = p.parent; if (p.parent == null) { root = replacement; } Else if (p == p.parent.left) { p.parent.left = replacement; } else { p.parent.right = replacement; } p.left = p.right = p.parent = null; if (p .color == BLACK) { fixAfterDeletion(replacement); } } else if (p.parent == null) { root = null; } else { // The node to be deleted has no child nodes // If the deleted node is black, You need to fix it first (p.color == BLACK) { fixAfterDeletion(p); } // Remove the node to be deleted from the tree if (p.parent != null) { if (p == p.parent. Left) { p.parent.left = null; } else if (p == p.parent.right) { p.parent.right = null; } p.parent = null; } } } private TreeNode Successor(TreeNode t) { if (Objects.isNull(t)) { return null; } if (t.right != null) { TreeNode p = t.right; while (p.left != null) { p = p.left; } return p; } else { TreeNode p = t.parent; TreeNode Ch = t; while (p != null && ch == p.right) { ch = p; p = p.parent; } return p; } } private void rotateLeft(TreeNode p) { if (Objects.nonNull(p)) { TreeNode r = p.right; p.right = r.left; if (r.left != null) { r.left.parent = p; } r.parent = p.parent; if (p.parent == null) { root = r; } else if (p.parent.left == p) { p.parent.left = r; } else { p.parent.right = r; } r.left = p; p.parent = r ; } } /** From CLR */ private void rotateRight(TreeNode p) { if (Objects.nonNull(p)) { TreeNode l = p.left; p.left = l.right; if (l.right != null) { l.right.parent = p; } l.parent = p.parent; if (p.parent == null) { root = l; } else if (p.parent.right == p) { p.parent.right = l; } else { p.parent.left = l; } l.right = p; p.parent = l ; } } /** From CLR */ private void fixAfterInsertion(TreeNode x) { x.color = RED; while (x != null && x != root && x.parent.color == RED) { if (parentOf(x) == leftOf(parentOf(parentOf(x)))) { TreeNode y = rightOf(parentOf(parentOf(x))); if (colorOf(y) == RED) { setColor(parentOf(x), BLACK); setColor(y, BLACK); setColor(parentOf(parentOf(x)) , RED); x = parentOf(parentOf(x)); } else { if (x == rightOf(parentOf(x))) { x = parentOf(x); rotateLeft(x); } setColor(parentOf(x) , BLACK); setColor(parentOf(parentOf(x)), RED); rotateRight(parentOf(parentOf(x))); } } else { TreeNode y = leftOf(parentOf(parentOf(x))); if (colorOf(y) == RED) { setColor(parentOf(x), BLACK); setColor(y, BLACK); setColor(parentOf(parentOf(x)) , RED); x = parentOf(parentOf(x)); } else { if (x == leftOf(parentOf(x))) { x = parentOf(x); rotateRight(x); } setColor(parentOf(x) , BLACK); setColor(parentOf(parentOf(x)), RED); rotateLeft(parentOf(parentOf(x))); } } } root.color = BLACK; } private void fixAfterDeletion(TreeNode x) { while (x != root && colorOf(x) == BLACK) { if (x == leftOf(parentOf(x))) { TreeNode Sib = rightOf(parentOf(x)); if (colorOf(sib) == RED) { setColor(sib, BLACK); setColor(parentOf(x), RED); rotateLeft(parentOf(x)); sib = rightOf( parentOf(x)); } if (colorOf(leftOf(sib)) == BLACK && colorOf(rightOf(sib)) == BLACK) { setColor(sib, RED); x = parentOf(x); } else { if (colorOf(rightOf(sib)) == BLACK) { setColor(leftOf(sib), BLACK); setColor(sib, RED); rotateRight(sib); sib = rightOf(parentOf(x)); } setColor(sib, colorOf(parentOf(x))); setColor(parentOf(x), BLACK); setColor(rightOf(sib), BLACK); rotateLeft(parentOf(x)); x = root; } } else { // symmetric TreeNode Sib = leftOf(parentOf(x)); if (colorOf(sib) == RED) { setColor(sib, BLACK); setColor(parentOf(x), RED); rotateRight(parentOf(x)); sib = leftOf( parentOf(x)); } if (colorOf(rightOf(sib)) == BLACK && colorOf(leftOf(sib)) == BLACK) { setColor(sib, RED); x = parentOf(x); } else { if (colorOf(leftOf(sib)) == BLACK) { setColor(rightOf(sib), BLACK); setColor(sib, RED); rotateLeft(sib); sib = leftOf(parentOf(x)); } setColor(sib, colorOf(parentOf(x))); setColor(parentOf(x), BLACK); setColor(leftOf(sib), BLACK); rotateRight(parentOf(x)); x = root; } } } setColor(x, BLACK) ; } private boolean colorOf(TreeNode p) { return (p == null ? BLACK : p.color); } private TreeNode parentOf(TreeNode p) { return (p == null ? null: p.parent); } private void setColor(TreeNode p, boolean c) { if (p != null) { p.color = c; } } private TreeNode leftOf(TreeNode p) { return (p == null) ? null: p.left; } private TreeNode rightOf(TreeNode p) { return (p == null) ? null: p.right; } private class TreeNode > { TreeNode Parent; TreeNode Left; TreeNode Right; T value; boolean color; public TreeNode(TreeNode Parent, TreeNode Left, TreeNode Right, T value) { this.parent = parent; this.left = left; this.right = right; this.value = value; this.color = RED; } @Override public String toString() { return value + ", " + (color == RED ? "r" : "b"); } }}

Finally, if you are also learning red black trees, I hope this article can help you. In addition, due to the complexity of the red-black tree itself, coupled with my limited level, it is inevitable that some mistakes will occur. If there is something wrong, I hope everyone will point it out and we will discuss it together.

5050 Single Color Led Strip

5050 Single Color Led Strip ,Single Color Led Strip,Single Color Led Strip Lights,Single Colour Led Strip

NINGBO SENTU ART AND CRAFT CO.,LTD. , https://www.lightworld-sentu.com